The World of Mental Math

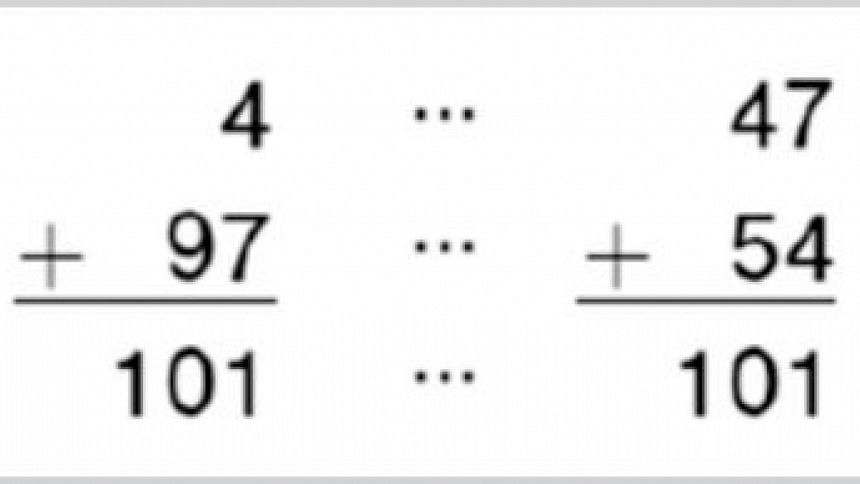
The boy arranged the numbers from 1 to 50. For the next 50, he reversed the order from 100 to 51. Each pair adds to 101. There are 50 such pairs. So, the sum total will be 100X50+50 = 5000+50 = 5050. That wasn't 'rocket 
science'!

The little boy was Karl Friedrich Gauss (1777-1855), one of the finest of German mathematicians. The beauty of numbers is they usually follow a pattern. Once the pattern is revealed, math can be fun. You don't need to be Gauss to find fun in numbers. 

Did you know if you keep on adding odd numbers, then each time you'll get a square? Let's see. 1+3 = 4, 2 Square. 1+3+5 = 9, 3 Square. 1+3+5+7= 16, 4 Square. Look at Figure 2.  Each number is a circle. See how the circles connect to make a square each time we add the next odd number.

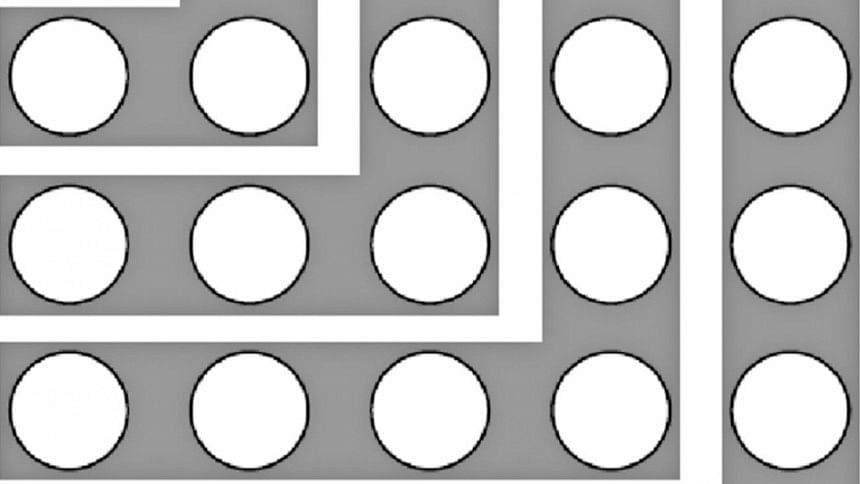
Except for 1, can you see each higher odd number as a reverse L as you look diagonally from the top left to the bottom right? Can you see a square each time you add a reverse L? The pattern: 1+3+5+7+9 now makes more sense because you can visualise the numbers and see how the pattern is constructed like a jigsaw puzzle. 

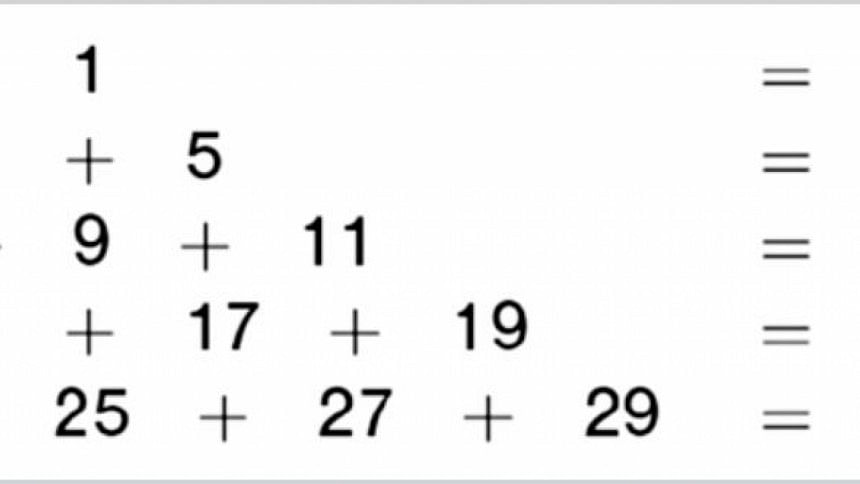
Let's now rearrange the odd numbers in a different pattern. 

1; (3+5); (7+9+11); (13+15+17+19); (21+23+25+27+29)
Add the numbers in each bracket. What do you get? 1 = 1 Cube; 8 = 2 Cube; 27 = 3 Cube; 64 = 4 Cube; 125 = 5 Cube. If you found the numbers confusing, then see the numbers as a pyramid. Can you make sense of the pattern, now?

Now, that we know the sum of successive odd numbers is a square, let's look at a very familiar table we all saw in school: the numbers table. 

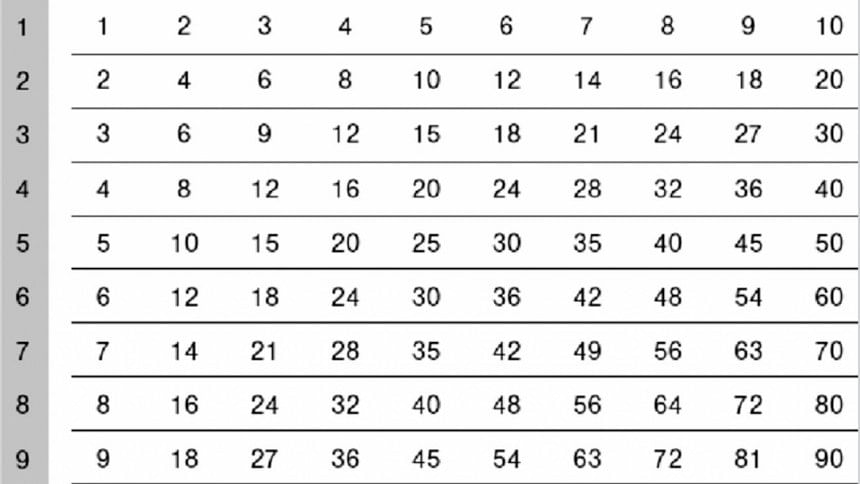
Let's choose a square: 7X7 = 49. Look at the numbers in the diagonal that crosses through 49 from the top right to the bottom left. What are the numbers? Both ways they are 48, 45, and 40. How less are they from 49? Are they less than 1, 4, and 9 respectively? Do you see a sequence of square numbers? Now let's consider 5X5 = 25. Performing the same, either way we get the numbers: 24, 21, 16, 9. How less are they from 25? Are they less than 1, 4, 9, and 16 respectively? Do you see a sequence of square numbers? 

Are you asking the question: why didn't I see these patterns at school? If you are, then here's a story. The poet, Sheikh Saadi of Shiraz in Persia (Iran) started writing at the age of 40. He lived for 80 years. Nine camels were needed to carry all his writings after his death. 
It's never too late to learn. Welcome to the world of mental math. YouTube and Wikipedia should keep you busy for quite some time.

Source: The Magic of Math: Solving for X and Figuring Out Why by Arthur Benjamin. Basic Books. Sep 2015. 

Asrar Chowdhury teaches economic theory and game theory in the classroom. Outside he listens to music and BBC Radio; follows Test Cricket; and plays the flute. He can be reached at: asrar.chowdhury@facebook.com